6 Root Symbol
- Have to construct √6 on the number line. Draw a horizontal line. Now take a point A on the line and mark at pint B so that AB = 6 unit 3. From the point B, mark C such that BC = 1 4. Now take a point O in between A and B such that OA = OC = (6 + 1)/2 = 7/3 = 3.5 unit 5. Now draw a circle having center at O and radius 3.5 units.
- You are very important to us. For any content/service related issues please contact on this number. Mon to Sat - 10 AM to 7 PM.
- In mathematics, a square root of a number x is a number y such that y 2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16, because 4 2 = (−4) 2 = 16.Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by, where the.
- Square Root (Symbol/sign/mark) Preview and HTML-code. With this tool, you can adjust the size, color, italic, and bold of Square Root(symbol). This tool is very convenient to help you preview the symbol, including viewing the details of the symbol display and the effect displayed on the web page.
Purplemath
First select the symbol then you can drag&drop or just copy&paste it anywhere you like. Alt-Codes can be typed on Microsoft Operating Systems: First make sure that numlock is on, Then press and hold the ALT key, While keeping ALT key pressed type the code for the symbol that you want and release the ALT key. Unicode codes can not be typed.
Just as with 'regular' numbers, square roots can be added together. But you might not be able to simplify the addition all the way down to one number. Just as 'you can't add apples and oranges', so also you cannot combine 'unlike' radical terms. In order to be able to combine radical terms together, those terms have to have the same radical part.
Simplify:
Since the radical is the same in each term (being the square root of three), then these are 'like' terms. This means that I can combine the terms.
MathHelp.com
I have two copies of the radical, added to another three copies. This gives mea total of five copies:
That middle step, with the parentheses, shows the reasoning that justifies the final answer. You probably won't ever need to 'show' this step, but it's what should be going through your mind.
Simplify:
The radical part is the same in each term, so I can do this addition. To help me keep track that the first term means 'one copy of the square root of three', I'll insert the 'understood' '1':
Don't assume that expressions with unlike radicals cannot be simplified. It is possible that, after simplifying the radicals, the expression can indeed be simplified.
Simplify:
To simplify a radical addition, I must first see if I can simplify each radical term. In this particular case, the square roots simplify 'completely' (that is, down to whole numbers):
Simplify:
I have three copies of the radical, plus another two copies, giving me— Wait a minute! I can simplify those radicals right down to whole numbers:
Don't worry if you don't see a simplification right away. If I hadn't noticed until the end that the radical simplified, my steps would have been different, but my final answer would have been the same:
Simplify:
Affiliate
I can only combine the 'like' radicals. The first and last terms contain the square root of three, so they can be combined; the middle term contains the square root of five, so it cannot be combined with the others. So, in this case, I'll end up with two terms in my answer.
I'll start by rearranging the terms, to put the 'like' terms together, and by inserting the 'understood' 1 into the second square-root-of-three term:
There is not, to my knowledge, any preferred ordering of terms in this sort of expression, so the expression should also be an acceptable answer.
Simplify:

As given to me, these are 'unlike' terms, and I can't combine them. But the 8 in the first term's radical factors as 2 × 2 × 2. This means that I can pull a 2 out of the radical. At that point, I will have 'like' terms that I can combine.
Simplify:
I can simplify most of the radicals, and this will allow for at least a little simplification:
Content Continues Below
Simplify:
These two terms have 'unlike' radical parts, and I can't take anything out of either radical. Then I can't simplify the expression any further and my answer has to be:
Expand:
To expand this expression (that is, to multiply it out and then simplify it), I first need to take the square root of two through the parentheses:
As you can see, the simplification involved turning a product of radicals into one radical containing the value of the product (being 2 × 3 = 6). You should expect to need to manipulate radical products in both 'directions'.
Expand:
6 Foot 6 Inches Symbol
As in the previous example, I need to multiply through the parentheses.
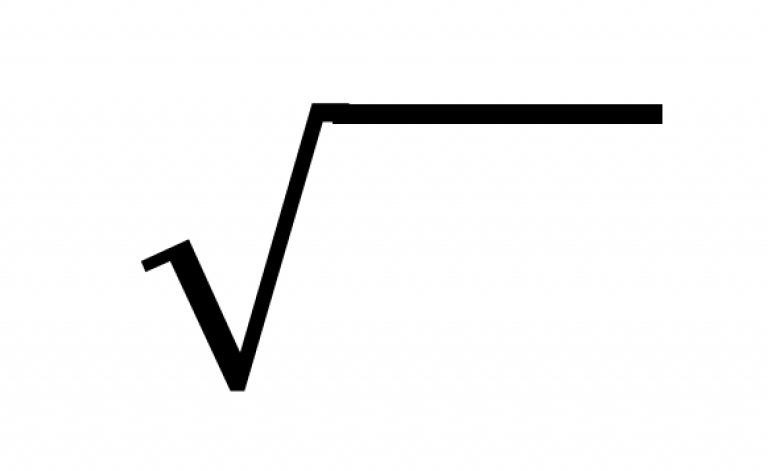
Expand:
It will probably be simpler to do this multiplication 'vertically'.
Simplifying gives me:
Affiliate
By doing the multiplication vertically, I could better keep track of my steps. You should use whatever multiplication method works best for you. But know that vertical multiplication isn't a temporary trick for beginning students; I still use this technique, because I've found that I'm consistently faster and more accurate when I do.
You can use the Mathway widget below to practice finding adding radicals. Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept 'preferences' cookies in order to enable this widget.
(Click 'Tap to view steps' to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/radicals3.htm
6 Feet Symbol
| Fraction Symbol | Fraction Name | Decimal | Hex |
|---|---|---|---|
| ¼ | Vulgar Fraction One Quarter | ¼ | ¼ |
| ½ | Vulgar Fraction One Half | ½ | ½ |
| ¾ | Vulgar Fraction Three Quarters | ¾ | ¾ |
| ⁄ | Fraction Slash | ⁄ | ⁄ |
| ⅐ | Vulgar Fraction One Seventh | ⅐ | ⅐ |
| ⅑ | Vulgar Fraction One Ninth | ⅑ | ⅑ |
| ⅒ | Vulgar Fraction One Tenth | ⅒ | ⅒ |
| ⅓ | Vulgar Fraction One Third | ⅓ | ⅓ |
| ⅔ | Vulgar Fraction Two Thirds | ⅔ | ⅔ |
| ⅕ | Vulgar Fraction One Fifth | ⅕ | ⅕ |
| ⅖ | Vulgar Fraction Two Fifths | ⅖ | ⅖ |
| ⅗ | Vulgar Fraction Three Fifths | ⅗ | ⅗ |
| ⅘ | Vulgar Fraction Four Fifths | ⅘ | ⅘ |
| ⅙ | Vulgar Fraction One Sixth | ⅙ | ⅙ |
| ⅚ | Vulgar Fraction Five Sixths | ⅚ | ⅚ |
| ⅛ | Vulgar Fraction One Eighth | ⅛ | ⅛ |
| ⅜ | Vulgar Fraction Three Eighths | ⅜ | ⅜ |
| ⅝ | Vulgar Fraction Five Eighths | ⅝ | ⅝ |
| ⅞ | Vulgar Fraction Seven Eighths | ⅞ | ⅞ |
| ⅟ | Fraction Numerator One | ⅟ | ⅟ |
| Fraction Symbol | Fraction Name | Decimal | Hex |
|---|---|---|---|
| ↉ | Vulgar Fraction Zero Thirds | ↉ | ↉ |
Copy and paste the Fraction symbol or use the unicode decimal, hex number or html entity in social websites, in your blog or in a document.
Fraction Symbol Preview Variations
| Fraction Symbol | Color | Italic Symbol |
|---|---|---|
| ¼ | Vulgar Fraction One Quarter red | ¼ |
| ¼ | Vulgar Fraction One Quarter orange | ¼ |
| ¼ | Vulgar Fraction One Quarter pink | ¼ |
| ¼ | Vulgar Fraction One Quarter green | ¼ |
| ¼ | Vulgar Fraction One Quarter royal blue | ¼ |
| ¼ | Vulgar Fraction One Quarter purple | ¼ |
| ½ | Vulgar Fraction One Half red | ½ |
| ½ | Vulgar Fraction One Half orange | ½ |
| ½ | Vulgar Fraction One Half pink | ½ |
| ½ | Vulgar Fraction One Half green | ½ |
| ½ | Vulgar Fraction One Half royal blue | ½ |
| ½ | Vulgar Fraction One Half purple | ½ |